學而思奧數天天練欄目每日精選一套高等難度的試題,各年級分開,配有詳細答案及試題解析,此類試題立足于杯賽真題、綜合應用和加深各知識點,適合一些志在競賽中奪取佳績的學生。
·本試題由武漢學而思奧數專職教師王帥老師精選、解析,以保證試題質量。
名師介紹: 畢業于北京師范大學數學與應用數學專業,小學數學奧林匹克二等獎,全國初中數學聯賽市級一等獎。
教學特色: 王帥老師,富有青春活力,熱愛教育事業,講課生動形象,注重引導孩子養成良好的學習習慣。王老師對學生非常有愛心和耐心,善于調動學生學習的積極性,抓住學生思路和心理,引導學生思考,鍛煉孩子自己動腦解決問題的能力,在講課中能及時與每個學生溝通,善于發現每個孩子身上的優點,幫助他們建立學習興趣和信心,培養他們嚴密的邏輯思維能力,找到適合每個孩子自己的學習方法,用生動有趣的語言配合細致的講解,帶領孩子們一步步成長。
·每道題的答題時間不應超過15分鐘
·您可以按“點擊下載適合打印版本試卷”獲得word版本試卷進行打印
小學一年級天天練答案:
因為14+7-4=17,要使等式右邊等于11可以采用多減、少加的辦法。通過改變運算符號就可以達到多減少加的目的。
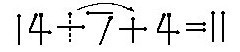
小學二年級天天練答案:
解:用數字代表盤子里的蘋果數,用由3個數字組成的數組表示不同的放置方式.如(7,0,0)表示:一個盤子里放7個蘋果,而另外兩個盤子里都空著不放.各種可能的放置情況如下:
(7,0,0)
(6,1,0)
(5,2,0),(5,1,1)
(4,3,0),(4,2,1)
(3,3,1),(3,2,2)
數一數,共有8種不同的放法.
小學三年級天天練答案:
解:題中有"至少"這一條.
用逆推法從最后的最少棋子情況逆推.先畫線段圖依次表示分棋子的過程,見下圖:
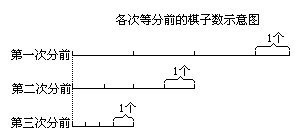
假設第三次分時,三等份中每分是1個棋子(最少),
則此次分前應是3+1=4個;4÷2=2,則第二次分前應是2×3+1=7個,注意7是奇數(第二次分前的棋子是第一次分后的兩份,應是偶數所以不應是7,可見前面假設不對).
再假設第三次分時每等份是2個棋子,也不行.
又假設第三次分時每等份是3個棋子,則有
3×3+1=10;
10÷2=5,5×3+1=16;
16÷2=8,8×3+1=25;
∴原來有棋子至少是25個.
小學四年級天天練答案:
分析:已知偶數個奇數的和是144.連續數的個數為偶數時,它的特點是首項與末項之和等于第二項與倒數第二項之和,等于第三項與倒數第三項之和……即每兩個數分為一組,八個數分成4組,每一組兩個數的和是144÷4=36.這樣可以確定出中間的兩個數,再依次求出其他各數。
解:①每組數之和:144÷4=36
②中間兩個數中較大的一個:(36+2)÷2=19
③中間兩個數中較小的一個:19-2=17
∴這八個連續奇數為11、13、15、17、19、21、23和25。
答:這八個連續奇數分別為:11、13、15、17、19、21、23和25。
小學五年級天天練答案:
解解:連結BD,將四邊形ABCD分成兩個部分S1與S2.連結FD,有S△FBD=S△DBC=S1所以S△CGF=S△DFC=2S1.
同理S△AEH=2S2,
因此S△AEH+S△CGF=2S1+2S2=2(S1+S2)=2×1=2.
同理,連結AC之后,可求出S△HGD+S△EBF=2所以四邊形EFGH的面積為2+2+1=5(平方單位)




