難度:★★★★
小學五年級奧數天天練:組合問題
下圖中有7個點和十條線段,一只甲蟲要從A點沿著線段爬到B點,要求任何線段和點不得重復經過.問:這只甲蟲最多有幾種不同的走法?
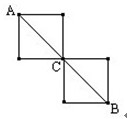
分析:甲蟲要從A點沿線段爬到B點,必經過C點,所以,完成這段路分兩步,即由A到C,再由C到B.而由A到C有三種走法,由C到B也有三種走法,所以,由乘法原理便可得到結論.
解:這只甲蟲從A到B共有3×3=9種不同的走法.
難度:★★★★★
小學五年級奧數天天練:組合問題
由數字0、1、2、3組成三位數,問:
1組成多少個不相等的三位數?
2組成多少個沒有重復數字的三位數?
分析:在確定由0、1、2、3組成的三位數的過程中,應該一位一位地去確定.所以,每個問題都可以看成是分三個步驟來完成.
①要求組成不相等的三位數.所以,數字可以重復使用,百位上,不能取0,故有3種不同的取法;十位上,可以在四個數字中任取一個,有4種不同的取法;個位上,也有4種不同的取法,由乘法原理,共可組成3×4×4=48個不相等的三位數.
②要求組成的三位數中沒有重復數字,百位上,不能取0,有3種不同的取法;十位上,由于百位已在1、2、3中取走一個,故只剩下0和其余兩個數字,故有3種取法;個位上,由于百位和十位已各取走一個數字,故只能在剩下的兩個數字中取,有2種取法,由乘法原理,共有3×3×2=18個沒有重復數字的三位數.
解:由乘法原理
② 可組成3×4×4=48(個)不同的三位數;
②共可組成3×3×2=18(個)沒有重復數字的三位數.



