·每道題的答題時(shí)間不應(yīng)超過(guò)15分鐘。答案明日公布!
難度:★★★★
小學(xué)六年級(jí)奧數(shù)天天練:計(jì)數(shù)
一個(gè)長(zhǎng)方形把平面分成兩部分,那么3個(gè)長(zhǎng)方形最多把平面分成多少部分?
【答案】
解答:一個(gè)長(zhǎng)方形把平面分成兩部分.第二個(gè)長(zhǎng)方形的每一條邊至多把第一個(gè)長(zhǎng)方形的內(nèi)部分成2部分,這樣第一個(gè)長(zhǎng)方形的內(nèi)部至多被第二個(gè)長(zhǎng)方形分成五部分.
同理,第二個(gè)長(zhǎng)方形的內(nèi)部至少被第一個(gè)長(zhǎng)方形分成五部分.這兩個(gè)長(zhǎng)方形有公共部分(如下圖,標(biāo)有數(shù)字9的部分).還有一個(gè)區(qū)域位于兩個(gè)長(zhǎng)方形外面,所以兩個(gè)長(zhǎng)方形至多把平面分成10部分.
第三個(gè)長(zhǎng)方形的每一條邊至多與前兩個(gè)長(zhǎng)方形中的每一個(gè)的兩條邊相交,故第一條邊被隔成五條小線段,其中間的三條小線段中的每一條線段都把前兩個(gè)長(zhǎng)方形內(nèi)部的某一部分一分為二,所以至多增加3×4=12個(gè)部分.而第三個(gè)長(zhǎng)方形的4個(gè)頂點(diǎn)都在前兩個(gè)長(zhǎng)方形的外面,至多能增加4個(gè)部分.
所以三個(gè)長(zhǎng)方形最多能將平面分成10+12+4=26.

難度:★★★★★
小學(xué)六年級(jí)奧數(shù)天天練:計(jì)數(shù)
一個(gè)圓上有12個(gè)點(diǎn)A1,A2,A3,…,A11,A12.以它們?yōu)轫旤c(diǎn)連三角形,使每個(gè)點(diǎn)恰好是一個(gè)三角形的頂點(diǎn),且各個(gè)三角形的邊都不相交.問(wèn)共有多少種不同的連法?
【答案】
解答:我們采用遞推的方法.
I如果圓上只有3個(gè)點(diǎn),那么只有一種連法.

Ⅱ如果圓上有6個(gè)點(diǎn),除A1點(diǎn)所在三角形的三頂點(diǎn)外,剩下的三個(gè)點(diǎn)一定只能在A1所在三角形的一條邊所對(duì)應(yīng)的圓弧上,表1給出這時(shí)有可能的連法.
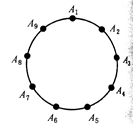
Ⅲ如果圓上有9個(gè)點(diǎn),考慮A1所在的三角形.此時(shí),其余的6個(gè)點(diǎn)可能分布在:
①A1所在三角形的一個(gè)邊所對(duì)的弧上;
②也可能三個(gè)點(diǎn)在一個(gè)邊所對(duì)應(yīng)的弧上,另三個(gè)點(diǎn)在另一邊所對(duì)的弧上.
在表2中用“+”號(hào)表示它們分布在不同的邊所對(duì)的弧.
如果是情形①,則由Ⅱ,這六個(gè)點(diǎn)有三種連法;
如果是情形②,則由①,每三個(gè)點(diǎn)都只能有一種連法.
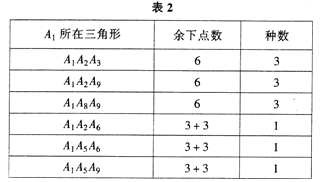
共有12種連法。
Ⅳ最后考慮圓周上有12個(gè)點(diǎn).同樣考慮A1所在三角形,剩下9個(gè)點(diǎn)的分布有三種可能:
①9個(gè)點(diǎn)都在同一段弧上:
②有6個(gè)點(diǎn)是在一段弧上,另三點(diǎn)在另一段弧上;
③每三個(gè)點(diǎn)在A1所在三角形的一條邊對(duì)應(yīng)的弧上.得到表3.
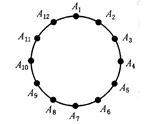

共有12×3+3×6+1=55種。
所以當(dāng)圓周上有12個(gè)點(diǎn)時(shí),滿足題意的連法有55種。



