學(xué)而思奧數(shù)天天練欄目每日精選中等、高等難度試題各一道。中難度試題適合一些有過思維基礎(chǔ)訓(xùn)練、考題學(xué)習(xí)經(jīng)歷，并且奧數(shù)成績(jī)中上的學(xué)生。高難度試題立足于杯賽真題、綜合應(yīng)用和加深各知識(shí)點(diǎn)，適合一些志在競(jìng)賽中奪取佳績(jī)的學(xué)生。

　　·本周試題由學(xué)而思奧數(shù)名師郭超凡精選、解析，以保證試題質(zhì)量。

　　·每周末，我們將一周試題匯總為word版本試卷，您可下載打印或在線閱讀。

　　·每道題的答題時(shí)間不應(yīng)超過15分鐘。答案明日公布！

　　難度：★★★★　

　　小學(xué)四年級(jí)奧數(shù)天天練：排列

　　5個(gè)人并排站成一排，其中甲必須站在中間有多少種不同的站法？

　　【答案】

　　解答：分析 由于甲必須站在中間，那么問題實(shí)質(zhì)上就是剩下的四個(gè)人去站其余四個(gè)位置的問題，是一個(gè)全排列問題，且n=4．
　　解：由全排列公式，共有

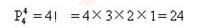
　　種不同的站法．



　　難度：★★★★★

　　小學(xué)四年級(jí)奧數(shù)天天練：加法原理

　　如下圖，要從A點(diǎn)沿線段走到B，要求每一步都是向右、向上或者向斜上方．問有多少種不同的走法？
 

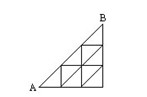
　　【答案】
 

　　【答案】

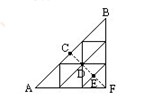
　　第一類，經(jīng)過C的路線，分為兩步，從A到C再?gòu)腃到B，從A到C有2條路可走，從C到B也有兩條路可走，由乘法原理，從A經(jīng)C到B共有2×2=4條不同的路線．

　　第二類，經(jīng)過D點(diǎn)的路線，分為兩步，從A到D有4條路，從D到B有4條路，由乘法原理，從A經(jīng)D到B共有4×4=16種不同的走法．

　　第三類，經(jīng)過E點(diǎn)的路線，分為兩步，從A到E再?gòu)腅到B，觀察發(fā)現(xiàn)．各有一條路．所以，從A經(jīng)E到B共有1種走法．

　　第四類，經(jīng)過F點(diǎn)的路線，從A經(jīng)F到B只有一種走法．

　　最后由加法原理即可求解．

　　解：如上右圖，從A到B共有下面的走法：

　　從A經(jīng)C到B共有2×2=4種走法；

　　從A經(jīng)D到B共有4×4=16種走法；

　　從A經(jīng)E到B共有1種走法；

　　從A經(jīng)F到B共有1種走法．

　　所以，從A到B共有：

　　4+16+1+1=22

　　種不同的走法．
 

名師介紹：

　　郭超凡老師畢業(yè)于武漢大學(xué)

　　初中數(shù)學(xué)聯(lián)賽國(guó)家級(jí)一等獎(jiǎng)、希望杯一等獎(jiǎng)，在其從事奧數(shù)教學(xué)的五年時(shí)間里，所教學(xué)生一半以上進(jìn)入"希望杯"、"華杯賽"復(fù)賽，并有3人獲得華杯賽一等獎(jiǎng)，2人獲得希望杯一等獎(jiǎng)，對(duì)小學(xué)奧數(shù)知識(shí)的體系架構(gòu)有很系統(tǒng)的了解。

　　教學(xué)特色

　　喜歡舉例子，夸張幽默；擅長(zhǎng)改題,潛移默化中學(xué)到知識(shí)。