數學家看問題,總想找規律.我們學數學,也要向他們學習.找規律,要從簡單的情況著手,仔細觀察,得到啟示,大膽猜想,找出一般規律,還要進行驗證,最后還需要證明(在小學階段不要求同學們進行證明).
例1 沿直尺的邊緣把紙上的兩個點連起來,這個圖形就叫做線段.這兩個點就叫線段的端點,如圖8—1—1所示.不難看出,線段也可以看成是直線上兩點間的部分.如果一條直線上標出11個點,如圖8—1—2所示,任何兩點間的部分都是一條線段,問共有多少條線段.
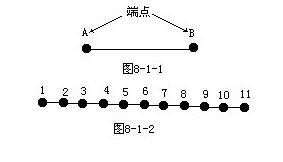
解:先從簡單的情況著手.
(1)畫一畫,數一數:(見圖8—1—3)
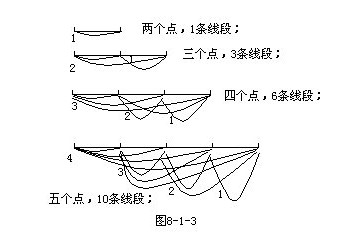
(2)試著分析:
2個點,線段條數:1=1
3個點,線段條數:3=2+1
4個點,線段條數:6=3+2+1
5個點,線段條數:10=4+3+2+1
(3)大膽猜想:一條直線上有若干點時線段的條數總是從1開始的一串自然數相加之和,其中最大的自然數比點數小1.
(4)進行驗證:對于更多點的情況,對猜想進行驗證,看猜想是否正確,如果正確,就增加了對猜想的信心.如:
6個點時:對不對?
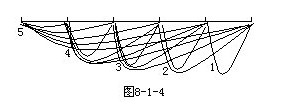
——對.見圖 8—1—4.
線段條數:5+4+3+2+1=15(條).
(5)應用規律:應用猜想到的規律解決更復雜的問題.
當直線上有11個點時,線段的條數應是:
10+9+8+7+6+5+4+3+2+1=55(條).
例2 如圖8—2中(1)~(5)所示兩條直線相交只有1個交點,3條直線相交最多有3個交點,4條直線相交最多有6個交點,……那么,11條直線相交最多有多少交點?
解:從簡單情況著手研究:
(1)畫一畫、數一數

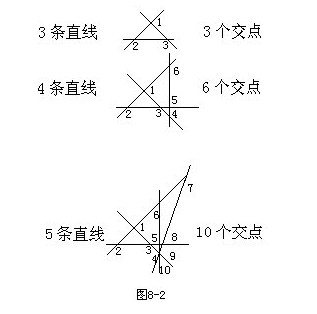
圖8-2
(2)試著分析:
直線條數 最多交點數
1 0
2 1=1
3 3=2+1
4 6=3+2+1
5 10=4+3+2+1
(3)大膽猜想:若干條直線相交時,最多的交點數是從1開始的一串自然數相加之和,其中最大的自然數比直線條數小1.
(4)進行驗證:見圖8—3.取6條直線相交,畫一畫,數一數,看一看最多交點個數與猜想的是否一致,若相符,則更增強了對猜想的信心.
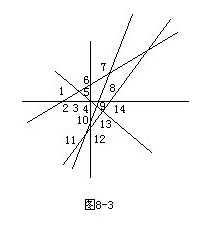
用猜想的算法進行計算:最多交點數應是
5+4+3+2+1=15(個).
(5)應用規律:應用猜想到的規律解決更復雜的問題.當有11條直線相交時,最多的交點數應是:
10+9+8+7+6+5+4+3+2+1=55(個).
例3 如圖8—4所示,一張大餅,切1刀最多切成2塊,切2刀最多切成4塊,切3刀最多切成7塊,……問切10刀最多切成多少塊?
解:從最簡單情況著手研究.
(1)畫一畫、數一數
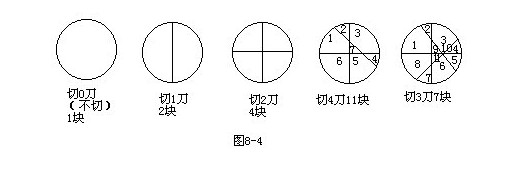
(2)試著分析:
所切刀數 切出的塊數
0 1
1 2=1+1
2 4=1+1+2
3 7=1+1+2+3
4 11=1+1+2+3+4
(3)大膽猜想:把一張大餅切若干刀時,切成的最多塊數等于從1開始的一串自然數相加之和加1.其中最大的自然數等于切的刀數.
(4)進行驗證:見圖8—5對大餅切5刀的情況用兩種方法求解,看結果是否一致,若一致則更增強了對猜想的信心.
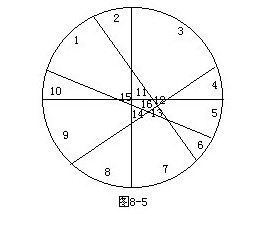
①數一數:16塊.
②算一算:1+1+2+3+4+5=16(塊).
(5)應用規律:把大餅切10刀時,最多切成的塊數是:
1+1+2+3+4+5+6+7+8+9+10
=1+55
=56(塊).



