例1 一只雞有一個(gè)頭2只腳,一只兔有一個(gè)頭4只腳.如果一個(gè)籠子里關(guān)著的雞和兔共有10個(gè)頭和26只腳,你知道籠子里有幾只雞、有幾只兔嗎?
解:這是古代的民間趣題,叫“雞兔同籠”問(wèn)題.見(jiàn)圖15-1(1)、(2)、(3).
①先畫10個(gè)頭:
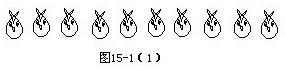
②每個(gè)頭下畫上兩條腿:
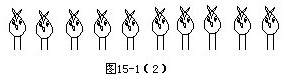
數(shù)一數(shù),共有20條腿,比題中給出的腿數(shù)少26-20=6條腿.

③給一些雞添上兩條腿,叫它變成兔.邊添腿邊數(shù),湊夠26條腿.
每把一只雞添上兩條腿,它就變成了兔,顯然添6條腿就變出來(lái)3只兔.這樣就得出答案,籠中有3只兔和7只雞.
例2 一輛自行車有2個(gè)輪子,一輛三輪車有3個(gè)輪子.車棚里放著自行車和三輪車共10輛,數(shù)數(shù)車輪共有26個(gè).問(wèn)自行車幾輛,三輪車幾輛?
解:發(fā)揮想像力和創(chuàng)造力,你可以畫一個(gè)簡(jiǎn)圖代表車身,見(jiàn)圖15-2(1)、(2)、(3).
①先畫10個(gè)車身:

②在每個(gè)車身下配上兩個(gè)輪子,它就成了自行車:

③數(shù)一數(shù)共20個(gè)車輪,比題中給出的輪子數(shù)少26-20=6個(gè)輪子,在自行車下面添輪子,每添一個(gè)輪子,這個(gè)自行車就成了三輪車.邊添邊湊數(shù),湊出26個(gè)輪子出來(lái).
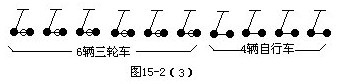
最后數(shù)一數(shù),共有6輛三輪車,4輛自行車.注意,用這種畫圖湊數(shù)法解題,很直觀,也比較快,為了使解題速度更快,可以把三個(gè)步驟合起來(lái),就能得出答案.
例3 一只蛐蛐6條腿,一只蜘蛛8條腿.現(xiàn)有蛐蛐和蜘蛛共10只,共有68條腿.問(wèn)蛐蛐幾只,蜘蛛幾只?
解:此題要想個(gè)更簡(jiǎn)單的辦法,見(jiàn)圖15-3(1)、(2).
①先畫10個(gè)頭,在每個(gè)頭下寫上數(shù)字“ 6”,代表6只腿,--即先假設(shè)10只都是蛐蛐,則如:

②數(shù)一數(shù),算一算,6×10=60,即共有60條腿,比題中給出的腿數(shù)少68-60=8條腿,所以就要在下面再添腿,每在一個(gè)頭下添2條腿(寫個(gè)“ 2”),它就變成了一只蜘蛛,共添上8條腿,就使總腿數(shù)湊夠68條腿了.

最后數(shù)一數(shù),共有4只蜘蛛,6只蛐蛐.
解這道題時(shí),我們用數(shù)字代表腿數(shù),使我們省去了畫“腿”的麻煩.其實(shí),也可以完全省去畫圖,我們只要把解題想法和算式摘出來(lái)就行了!
第一步,先把10只全部看成是蛐蛐,那么一共就有:
6×10=60條腿.
第二步,算一算少了多少條腿?
少了68-60=8條腿.
第三步,把一個(gè)蛐蛐給它添上2條腿,使它變成了蜘蛛,可以變成幾只蜘蛛呢?
8÷2=4只(蜘蛛),
第四步,再算出蛐蛐的只數(shù)出來(lái):
10-4=6只(蛐蛐).
這樣一來(lái),我們就不必借助于畫圖的直觀形象,也可以解這類題目了.如果能這樣,我們的思維能力就又提高一步了!特別重要的是,我們這樣就可以不用“湊數(shù)”的嘗試方法了.
例4 籠中有兔又有雞,數(shù)數(shù)腿36,數(shù)數(shù)腦袋11,問(wèn)幾只兔子幾只雞?
解:方法 1:先用畫圖湊數(shù)法解,見(jiàn)圖 15-4(1)、(2)、(3).
①先畫11個(gè)頭:

②再在頭下填腿:
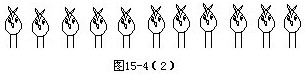
③數(shù)一數(shù),共有2×11=22條腿.還少36-22=14條腿,每添2條腿,就使一只雞變成兔.
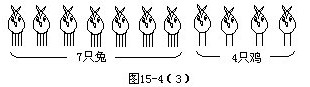
數(shù)一數(shù),共變出了7只兔:14÷2=7.
最后數(shù)一數(shù),籠中共有7只兔,4只雞.
方法2:
①把11只全部看成雞,共有2×11=22條腿.
②比題中給出的腿數(shù)少了36-22=14條腿.
③給一只雞添2條腿使它變成一只兔,共變成:
14÷2=7只(兔).
④再算出雞數(shù)為:11-7=4只(雞).
例5 今有五分的和一角的兩種汽車票,共10張,總錢數(shù)是七角五分.問(wèn)每種各幾張?
解:方法1:分步列式法:
若10張全是5分的,錢數(shù)應(yīng)為:
5×10=50分,即5角.
比題中給的錢數(shù)少:75-50=25分.
每給一張5分車票加5分,它就變成了1張1角車票了,共變出:
25÷5=5張(1角車票)
5分車票有10-5=5張(5分車票).
方法2:用畫圖湊數(shù)法.見(jiàn)圖15-5(1)、(2).
①先都畫成5分的:

②算一算共5×10=50分(即5角).
比題中給的錢數(shù)少75分-50=25分.
③給有些5分車票加錢,使它變成1角的,湊出總錢數(shù)與題目相符合.

最后數(shù)一數(shù),可知1角的車票5張,5分的車票5張.



