奧數(shù) > 小學(xué)資源庫 > 奧數(shù)天天練 > 四年級奧數(shù)天天練 > 文章列表 > 正文
2011-08-23 15:17:39 下載試卷
【分析】 因為100個連續(xù)自然數(shù)中的所有第奇數(shù)個自然數(shù)構(gòu)成了公差為2的等差數(shù)列，所以常規(guī)的思路是把這50個自然數(shù)求出來之后再求和，這是一種從局部到整體的分析策略.(動筆算算看!)
運用對應(yīng)的思想去分析卻別有一番天地.
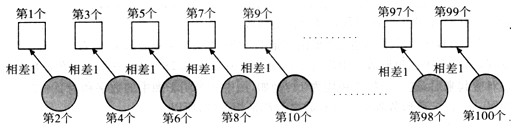
如上圖所示，我們雖然不知道這lOO個連續(xù)自然數(shù)具體是幾，但我們可以把這100個連續(xù)自然數(shù)進(jìn)行配對：(第1個，第2個)、(第3個，第4個)、…、(第99個，第100個)
配對后，顯然每一對自然數(shù)相差1.那么所有“第奇數(shù)個自然數(shù)的和”比所有“第偶數(shù)個自然數(shù)的和”少50. 由此問題轉(zhuǎn)化為一個和差問題，而所有第奇數(shù)個自然數(shù)的和(8450—50)÷2=4200.
來源：杭州奧數(shù)網(wǎng)
| 星期日 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 | 星期六 |
|---|---|---|---|---|---|---|
| 27 | 28 | 29 | 30 | 1 填數(shù) |
2 填數(shù) |
3 數(shù)一數(shù) |
| 4 數(shù)一數(shù) |
5 一筆畫 |
6 枚舉法 |
7 嘗試法 |
8 最短路線 |
9 火柴棒 |
10 火柴棒 |
| 11 火柴棒 |
12 火柴棒 |
13 火柴棒 |
14 火柴棒 |
15 火柴棒 |
16 年齡問題 |
17 年齡問題 |
| 18 年齡問題 |
19 年齡問題 |
20 年齡問題 |
21 年齡問題 |
22 年齡問題 |
23 邏輯問題 |
24 邏輯問題 |
| 25 應(yīng)用題 |
26 邏輯問題 |
27 邏輯問題 |
28 平均數(shù) |
29 平均數(shù) |
30 平均數(shù) |
31 平均數(shù) |
| 星期日 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 | 星期六 |
|---|---|---|---|---|---|---|
| 1 智力題 |
2 智力題 |
3 算式謎 |
4 算式謎 |
5 應(yīng)用題 |
6 應(yīng)用題 |
7 圖形分割 |
| 8 數(shù)字謎 |
9 應(yīng)用題 |
10 排隊問題 |
11 邏輯推理 |
12 應(yīng)用題 |
13 計算 |
14 排隊問題 |
| 15 排隊問題 |
16 排隊問題 |
17 排隊問題 |
18 排隊問題 |
19 排隊問題 |
20 排隊問題 |
21 植樹問題 |
| 22 植樹問題 |
23 植樹問題 |
24 植樹問題 |
25 植樹問題 |
26 找規(guī)律 |
27 找規(guī)律 |
28 找規(guī)律 |
| 29 找規(guī)律 |
30 找規(guī)律 |
31 找規(guī)律 |
1 | 2 | 3 | 4 |
| 星期日 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 | 星期六 |
|---|---|---|---|---|---|---|
| 29 | 30 | 31 | 1 枚舉法 |
2 嘗試法 |
3 最短路線 |
4 等量代換 |
| 5 植樹問題 |
6 應(yīng)用題 |
7 火柴棒 |
8 火柴棒 |
9 火柴棒 |
10 火柴棒 |
11 火柴棒 |
| 12 火柴棒 |
13 火柴棒 |
14 年齡問題 |
15 年齡問題 |
16 年齡問題 |
17 年齡問題 |
18 年齡問題 |
| 19 年齡問題 |
20 年齡問題 |
21 應(yīng)用題 |
22 智力題 |
23 優(yōu)化問題 |
24 應(yīng)用題 |
25 找規(guī)律 |
| 26 應(yīng)用題 |
27 找規(guī)律 |
28 巧算 |
1 | 2 | 3 | 4 |
| 星期日 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 | 星期六 |
|---|---|---|---|---|---|---|
| 26 | 27 | 28 | 1 趣味題 |
2 趣味題 |
3 趣味題 |
4 趣味題 |
| 5 趣味題 |
6 趣味題 |
7 趣味題 |
8 思維邏輯 |
9 思維邏輯 |
10 思維邏輯 |
11 思維邏輯 |
| 12 思維邏輯 |
13 思維邏輯 |
14 思維邏輯 |
15 行程問題 |
16 行程問題 |
17 行程問題 |
18 行程問題 |
| 19 行程問題 |
20 行程問題 |
21 行程問題 |
22 應(yīng)用題 |
23 應(yīng)用題 |
24 應(yīng)用題 |
25 應(yīng)用題 |
| 26 應(yīng)用題 |
27 應(yīng)用題 |
28 應(yīng)用題 |
29 平均數(shù) |
30 枚舉法 |
31 周期問題 |
1 |
| 星期日 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 | 星期六 |
|---|---|---|---|---|---|---|
| 26 | 27 | 28 | 29 | 30 | 31 | 1 周期問題 |
| 2 火柴棒 |
3 應(yīng)用題 |
4 找規(guī)律 |
5 周期問題 |
6 應(yīng)用題 |
7 邏輯問題 |
8 填算符 |
| 9 數(shù)獨 |
10 計數(shù) |
11 推理 |
12 周期問題 |
13 數(shù)獨 |
14 找規(guī)律 |
15 植樹問題 |
| 16 計數(shù) |
17 計數(shù) |
18 植樹問題 |
19 數(shù)一數(shù) |
20 應(yīng)用題 |
21 自然數(shù)串 |
22 數(shù)一數(shù) |
| 23 應(yīng)用題 |
24 還原問題 |
25 圖形變變變 |
26 邏輯推理 |
27 填數(shù)字 |
28 有余除法 |
29 周期問題 |
| 30 歸一問題 |
1 | 2 | 3 | 4 | 5 | 6 |
| 星期日 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 | 星期六 |
|---|---|---|---|---|---|---|
| 30 | 1 應(yīng)用題 |
2 應(yīng)用題 |
3 應(yīng)用題 |
4 應(yīng)用題 |
5 應(yīng)用題 |
6 應(yīng)用題 |
| 7 應(yīng)用題 |
8 付錢的方法 |
9 付錢的方法 |
10 付錢的方法 |
11 付錢的方法 |
12 付錢的方法 |
13 付錢的方法 |
| 14 摸彩球 |
15 摸彩球 |
16 摸彩球 |
17 摸彩球 |
18 摸彩球 |
19 巧算速算 |
20 巧算速算 |
| 21 巧算速算 |
22 天平平衡 |
23 合理分組 |
24 合理分組 |
25 合理分組 |
26 合理分組 |
27 合理分組 |
| 28 找規(guī)律 |
29 找規(guī)律 |
30 找規(guī)律 |
31 找規(guī)律 |
1 | 2 | 3 |
| 星期日 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 | 星期六 |
|---|---|---|---|---|---|---|
| 28 | 29 | 30 | 31 | 1 巧算 |
2 應(yīng)用題 |
3 應(yīng)用題 |
| 4 應(yīng)用題 |
5 應(yīng)用題 |
6 找規(guī)律 |
7 找規(guī)律 |
8 數(shù)一數(shù) |
9 移多補少 |
10 植樹問題 |
| 11 植樹問題 |
12 數(shù)字謎 |
13 數(shù)字謎 |
14 整式加減 |
15 整式加減 |
16 應(yīng)用題 |
17 應(yīng)用題 |
| 18 簡單推理 |
19 簡單推理 |
20 年齡問題 |
21 年齡問題 |
22 火柴棒 |
23 火柴棒 |
24 找規(guī)律 |
| 25 找規(guī)律 |
26 還原問題 |
27 還原問題 |
28 計算 |
29 計算 |
30 計算 |
1 |
| 星期日 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 | 星期六 |
|---|---|---|---|---|---|---|
| 25 | 26 | 27 | 28 | 29 | 30 | 1 應(yīng)用題 |
| 2 應(yīng)用題 |
3 應(yīng)用題 |
4 應(yīng)用題 |
5 應(yīng)用題 |
6 應(yīng)用題 |
7 應(yīng)用題 |
8 數(shù)數(shù)與計數(shù) |
| 9 數(shù)數(shù)與計數(shù) |
10 數(shù)數(shù)與計數(shù) |
11 數(shù)數(shù)與計數(shù) |
12 數(shù)數(shù)與計數(shù) |
13 行程問題 |
14 觀察數(shù)列 |
15 寫數(shù)列 |
| 16 等差數(shù)列 |
17 周期問題 |
18 找規(guī)律 |
19 找規(guī)律 |
20 找規(guī)律 |
21 填數(shù)字 |
22 等量代換 |
| 23 等量代換 |
24 等量代換 |
25 等量代換 |
26 等量代換 |
27 逆序推理法 |
28 逆序推理法 |
29 逆序推理法 |
| 30 逆序推理法 |
31 逆序推理法 |
1 | 2 | 3 | 4 | 5 |
| 星期日 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 | 星期六 |
|---|---|---|---|---|---|---|
| 30 | 31 | 1 應(yīng)用題 |
2 邏輯思維 |
3 排隊問題 |
4 年齡問題 |
5 火柴棒問題 |
| 6 邏輯問題 |
7 邏輯問題 |
8 應(yīng)用題 |
9 邏輯問題 |
10 填算符 |
11 應(yīng)用題 |
12 年齡問題 |
| 13 應(yīng)用題 |
14 應(yīng)用題 |
15 應(yīng)用題 |
16 應(yīng)用題 |
17 應(yīng)用題 |
18 應(yīng)用題 |
19 應(yīng)用題 |
| 20 火柴棒問題 |
21 報數(shù) |
22 數(shù)字游戲 |
23 填符號 |
24 想一想 |
25 想一想 |
26 應(yīng)用題 |
| 27 速算 |
28 速算 |
29 速算 |
30 數(shù)一數(shù) |
31 應(yīng)用題 |
1 | 2 |
| 星期日 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 | 星期六 |
|---|---|---|---|---|---|---|
| 27 | 28 | 29 | 30 | 31 | 1 火柴棒 |
2 火柴棒 |
| 3 火柴棒 |
4 火柴棒 |
5 火柴棒 |
6 火柴棒 |
7 火柴棒 |
8 年齡問題 |
9 年齡問題 |
| 10 年齡問題 |
11 年齡問題 |
12 年齡問題 |
13 年齡問題 |
14 年齡問題 |
15 植樹問題 |
16 植樹問題 |
| 17 植樹問題 |
18 植樹問題 |
19 植樹問題 |
20 植樹問題 |
21 植樹問題 |
22 思維邏輯 |
23 思維邏輯 |
| 24 思維邏輯 |
25 思維邏輯 |
26 思維邏輯 |
27 找規(guī)律 |
28 找規(guī)律 |
29 找規(guī)律 |
30 找規(guī)律 |
| 星期日 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 | 星期六 |
|---|---|---|---|---|---|---|
| 1 行程問題 |
2 行程問題 |
3 算式謎 |
4 算式謎 |
5 年齡問題 |
6 加乘原理 |
7 加乘原理 |
| 8 速算巧算 |
9 速算巧算 |
10 找規(guī)律 |
11 找規(guī)律 |
12 圖形計數(shù) |
13 圖形計數(shù) |
14 算式謎 |
| 15 算式謎 |
16 巧算 |
17 巧算 |
18 比較 |
19 比較 |
20 計算 |
21 計算 |
| 22 定義新運算 |
23 定義新運算 |
24 應(yīng)用題 |
25 巧算 |
26 巧算 |
27 計算 |
28 應(yīng)用題 |
| 29 應(yīng)用題 |
30 平均數(shù) |
31 牛吃草 |
1 | 2 | 3 | 4 |
| 星期日 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 | 星期六 |
|---|---|---|---|---|---|---|
| 29 | 30 | 31 | 1 定義新運算 |
2 等差數(shù)列 |
3 排列組合 |
4 和差問題 |
| 5 平均數(shù)問題 |
6 應(yīng)用題 |
7 逆推問題 |
8 植樹問題 |
9 雞兔同籠 |
10 盈虧問題 |
11 沏茶問題 |
| 12 排列組合 |
13 面積問題 |
14 邏輯推理 |
15 行程問題 |
16 行程問題 |
17 面積問題 |
18 盈虧問題 |
| 19 雞兔同籠 |
20 植樹問題 |
21 計算 |
22 行程問題 |
23 平均數(shù) |
24 和差問題 |
25 排列組合 |
| 26 等差數(shù)列 |
27 定義新運算 |
28 奇數(shù)與偶數(shù) |
29 乘法原理 |
30 和差問題 |
1 | 2 |
歡迎掃描二維碼
關(guān)注奧數(shù)網(wǎng)微信
ID：aoshu_2003
歡迎掃描二維碼
關(guān)注中考網(wǎng)微信
ID：zhongkao_com
歡迎掃描二維碼
奧數(shù)學(xué)習(xí)社
奧數(shù)網(wǎng)管方服務(wù)號
歡迎掃描二維碼
關(guān)注初三學(xué)習(xí)社
中考網(wǎng)官方服務(wù)號