我們學(xué)過的常用運算有:+、-、×、÷等.
如:2+3=5
2×3=6
都是2和3,為什么運算結(jié)果不同呢?主要是運算方式不同,實際是對應(yīng)法則不同.可見一種運算實際就是兩個數(shù)與一個數(shù)的一種對應(yīng)方法,對應(yīng)法則不同就是不同的運算.當(dāng)然,這個對應(yīng)法則應(yīng)該是對任意兩個數(shù),通過這個法則都有一個唯一確定的數(shù)與它們對應(yīng).只要符合這個要求,不同的法則就是不同的運算.在這一講中,我們定義了一些新的運算形式,它們與我們常用的“+”,“-”,“×”,“÷”運算不相同.
我們先通過具體的運算來了解和熟悉“定義新運算”.
例1 設(shè)a、b都表示數(shù),規(guī)定a△b=3×a—2×b,
①求 3△2, 2△3;
②這個運算“△”有交換律嗎?
③求(17△6)△2,17△(6△2);
④這個運算“△”有結(jié)合律嗎?
⑤如果已知4△b=2,求b.
分析解定義新運算這類題的關(guān)鍵是抓住定義的本質(zhì),本題規(guī)定的運算的本質(zhì)是:用運算符號前面的數(shù)的3倍減去符號后面的數(shù)的2倍.解:① 3△2= 3×3-2×2=9-4= 5
2△3=3×2-2×3=6-6=0.
②由①的例子可知“△”沒有交換律.
③要計算(17△6)△2,先計算括號內(nèi)的數(shù),有:17△6=3×17-2×6=39;再計算第二步
39△2=3 × 39-2×2=113,
所以(17△6)△2=113.
對于17△(6△2),同樣先計算括號內(nèi)的數(shù),6△2=3×6-2×2=14,其次
17△14=3×17-2×14=23,
所以17△(6△2)=23.
④由③的例子可知“△”也沒有結(jié)合律.⑤因為4△b=3×4-2×b=12-2b,那么12-2b=2,解出b=5.
例2 定義運算※為a※b=a×b-(a+b),①求5※7,7※5;
②求12※(3※4),(12※3)※4;
③這個運算“※”有交換律、結(jié)合律嗎?④如果3※(5※x)=3,求x.
解:① 5※7=5×7-(5+7)=35-12=23,7※ 5= 7×5-(7+5)=35-12=23.
②要計算12※(3※4),先計算括號內(nèi)的數(shù),有:3※4=3×4-(3+4)=5,再計算第二步12※5=12×5-(12+5)=43,
所以 12※(3※4)=43.
對于(12※3)※4,同樣先計算括號內(nèi)的數(shù),12※3=12×3-(12+3)=21,其次
21※4=21×4-(21+4)=59,所以(12※ 3)※4=59.③由于a※b=a×b-(a+b);
b※a=b×a-(b+a)
=a×b-(a+b)(普通加法、乘法交換律)
所以有a※b=b※a,因此“※”有交換律.
由②的例子可知,運算“※”沒有結(jié)合律.
④5※x=5x-(5+x)=4x-5;
3※(5※x)=3※(4x-5)
=3(4x-5)-(3+4x-5)
=12x-15-(4x-2)
= 8x- 13
那么 8x-13=3
解出x=2.

③這個運算有交換律和結(jié)合律嗎?




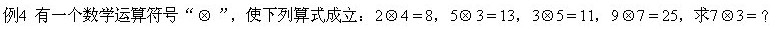
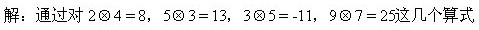
的觀察,找到規(guī)律:
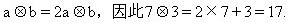
例5 x、y表示兩個數(shù),規(guī)定新運算“*”及“△”如下:x*y=mx+ny,x△y=kxy,其中 m、n、k均為自然數(shù),已知 1*2=5,(2*3)△4=64,求(1△2)*3的值.
分析 我們采用分析法,從要求的問題入手,題目要求1△2)*3的值,首先我們要計算1△2,根據(jù)“△”的定義:1△2=k×1×2=2k,由于k的值不知道,所以首先要計算出k的值.k值求出后,l△2的值也就計算出來了,我們設(shè)1△2=a.
(1△2)*3=a*3,按“*”的定義: a*3=ma+3n,在只有求出m、n時,我們才能計算a*3的值.因此要計算(1△2)* 3的值,我們就要先求出 k、m、n的值.通過1*2 =5可以求出m、n的值,通過(2*3)△4=64求出 k的值.
解:因為1*2=m×1+n×2=m+2n,所以有m+2n
=5.又因為m、n均為自然數(shù),所以解出:
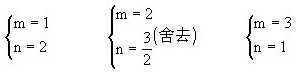
①當(dāng)m=1,n=2時:
(2*3)△4=(1×2+2×3)△4
=8△4=k×8×4=32k
有32k=64,解出k=2.
②當(dāng)m=3,n=1時:
(2*3)△4=(3×2+1×3)△4
=9△4=k×9×4=36k

所以m=l,n=2,k=2.
(1△2)*3=(2×1×2)*3
=4*3
=1×4+2×3
=10.
在上面這一類定義新運算的問題中,關(guān)鍵的一條是:抓住定義這一點不放,在計算時,嚴(yán)格遵照規(guī)定的法則代入數(shù)值.還有一個值得注意的問題是:定義一個新運算,這個新運算常常不滿足加法、乘法所滿足的運算定律,因此在沒有確定新運算是否具有這些性質(zhì)之前,不能運用這些運算律來解題.



