1.解:利用例1得到的規律可知:一條直線上有若干點時,線段的條數是從1開始的一串自然數相加之和,其中最大的自然數比點數小1.
1+2+3+4+5+6+7+8+9+10+11+12
=78(條).
2.解:利用例2得到的規律可知,有若干條直線相交時,最多的交點數是從1開始的一串自然數相加之和,其中最大的自然數比直線條數小1.
1+2+3+4+5+6+7+8+9+10+11+12
=78(個).
3.解:利用例3得到的規律可知,把一張大餅切若干刀時,切成的最多塊數,等于從1開始的一串自然數相加之和加1,其中最大的自然數等于切的刀數.
1+1+2+3+4+5+6+7+8+9+10+11+12
=1+78
=79(塊).
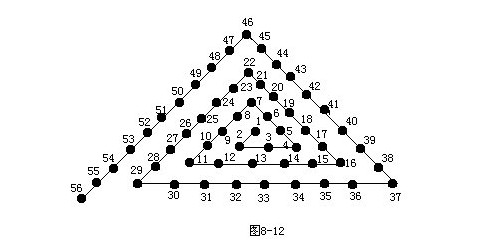
4.解:方法1:觀察圖8—12,仔細分析找規律.
第一個拐彎處 2=1+1
第二個拐彎處 4=1+1+2
第三個拐彎處 7=1+1+2+3
第四個拐彎處 11=1+1+2+3+4
第五個拐彎處 16=1+1+2+3+4+5
發現規律:拐彎處的數是從1開始的一串自然數相加之和再加1,在第幾個拐彎處,就加到第幾個自然數.
所以第十個拐彎處的數是:
1+1+2+3+4+5+6+7+8+9+10=56.
方法2:由于此題比較簡單,把圖形畫出來(圖8—12),按要求把自然數排列在三角形的邊上,答案也是56.
5.解:對簡單的情況,仔細觀察、分析,大膽猜想,找出規律,用于解決復雜的情況.如圖8—13所示:切一刀,1種切法:1=1
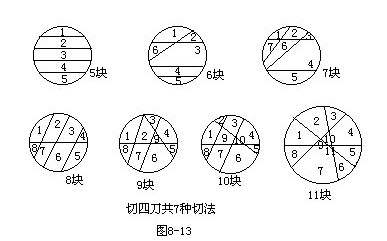
切兩刀,2種切法:2=1+1
切三刀,4種切法:4=1+1+2
大膽猜想,切四刀的切法數應為:
1+1+2+3=7種切法.
進行驗證(實際切切看):
應用得到的規律,求得切十一刀的不同切法數為:1+1+2+3+4+5+6+7+8+9+10
=1+55
=56(種).



