學而思奧數天天練欄目每日精選中等、高等難度試題各一道。中難度試題適合一些有過思維基礎訓練、考 題學習經歷,并且奧數成績中上的學生。高難度試題立足于杯賽真題、綜合應用和加深各知識點,適合一些志在競賽中 奪取佳績的學生。
·本周試題由學而思奧數名師精選、解析,以保證試題質量。
·每周末,我們將一周試題匯總為word版本試卷,您可下載打印或在線閱讀。
·每道題的答題時間不應超過15分鐘。答案明日公布!
難度:★★★★
整數推理問題
有30個2分硬幣和8個5分硬幣,這些硬幣值的總和正好是1元。用這些硬幣不能組成1元之內的幣值是_______。
【答案】
1分、3分、97分和99分四種。
解析:因為硬幣有2分、5分兩種,顯然不能組成1分和3分幣值。
同時根據硬幣的總額為1元=100分的條件可知,也不可能組成100-1=99(分)和100-3=97(分)幣值。
因此,用這些硬幣不能組成1元之內的幣值是1分、3分、97分和99分。
難度:★★★★★
a是一個自然數,已知a與a+1的各位數字之和都能被7整除,那么這樣的自然數a最小是_______。
【答案】
最小a是69999。
解析:根據題意, a+1必須在a的基礎上進位,不然a和a+1的各位數字之和就成為兩個相鄰的自然數,顯然不可能同時被7整除,這樣a的個位數字只能是9,而a+1的個位數字必然是0。
首先, a+1不會是兩位數,因為個位數字是0,各位數字之和能被7整除的兩位數只有70;而69的各位數字之和不能被7整除。
其次,考慮a+1是三位數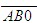 ,此處B只能是0,不然a的各位數字之和一定是A+(B-1)+9=A+B+8,而a+1的各位數字之和是A+B,這兩個數字和不會同時被7整除.當B是0時,A只能是7,即a+1等于700,但a等于699,各位數字之和不能被7整除,說明a+1不能是三位數。
,此處B只能是0,不然a的各位數字之和一定是A+(B-1)+9=A+B+8,而a+1的各位數字之和是A+B,這兩個數字和不會同時被7整除.當B是0時,A只能是7,即a+1等于700,但a等于699,各位數字之和不能被7整除,說明a+1不能是三位數。
采用類似的辦法可知, a+1不會是四位數。說明a+1至少是五位數,而且末尾四位也必須都是0,即a+1至少是五位數,而且末尾四位也必須都是0,即a+1=70000,此時a=69999.均滿足要求,說明符合條件的最小a是69999。



