小學(xué)奧數(shù)難題分析:豎式填空之巧填除法
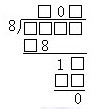
例1 一個(gè)三位數(shù),其十位數(shù)字是0,且能被一個(gè)一位數(shù)整除;如果被另一個(gè)一位數(shù)除則余3。請(qǐng)?zhí)钌纤羞m合的情況。
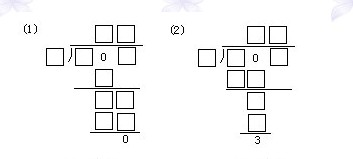
根據(jù)所有條件,全面分析,有序思考:
式(1)中,由除數(shù)與商的首位數(shù)之積是一個(gè)數(shù)字,知被除數(shù)的百位數(shù)字為1;

式(2)中,由余數(shù)是3,且除數(shù)與商的末位數(shù)的積是一位數(shù)和“余數(shù)必小于除數(shù)”,知除數(shù)只能為4、5、6,被除數(shù)的前兩位數(shù)為10,除數(shù)只能為5,被除數(shù)的末位數(shù)字為8,這個(gè)數(shù)為108;
因?yàn)?08能被2、3、4、6、9整除,但除數(shù)為2不符合式(1)的書(shū)寫形式。答案為:

例2
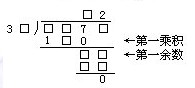
由第一乘積和第一余數(shù),知除數(shù)是35;商的十位數(shù)字可能是6或4。
商是62不合題意,則除數(shù)是35,商為42。
例3 下式可整除,請(qǐng)?jiān)凇踔刑钸M(jìn)適當(dāng)?shù)臄?shù)。
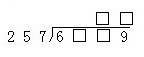
對(duì)比聯(lián)想,逆向思考——轉(zhuǎn)除為乘。

顯然,A位只能為7。
B=5,是一定的。C只能是2,到此整個(gè)算式解開(kāi)。
例4 第五冊(cè)數(shù)學(xué)思考題:
首尾觀察:

觀察式(1),知商的百位上是6;再觀察式(2),知商的個(gè)位上是2。則被除數(shù)為4816。
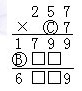
例5 美國(guó)小學(xué)數(shù)學(xué)奧林匹克,第四次(1981年 2月)題 5:在右邊的除法算式中,方格表示擦掉的數(shù)字,A和B表示商的數(shù)字。求A和B的值。 A B A B
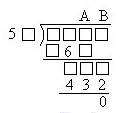
由B×5□=432,知B=8;進(jìn)而知A×54=□6□,A=3。



