五年級奧數題及答案解析:行程問題
1.一只小船從甲地到乙地往返一次共需要2小時,回來時順水比去時每小時多行駛8 千米,因此第2小時比第1小時多行駛6千米,則甲、乙兩地的距離為多少千米?
【分析】20+3×20=80,20-1×20=0,所以若20道題全答對可得最高分80分,若全答錯得最低分0分.由于每一道題都得奇數分或扣奇數分,20個奇數相加減所得結果為偶數,再加上20分基礎分仍為偶數,所以每個人所得分值都為偶數.而0到80之間共41個偶數,所以一共有41種分值,即41個抽屜.1978÷41=48……10,所以至少有49人得分相同.
2.甲、乙兩車往返于A、B兩地之間。甲車去時的速度是每小時60千米,回來時速度是每小時80千米。乙車往返的速度都是每小時70千米。甲、乙往返一次所用時間的比是 .
【分析】設[60,70,80] =1680(千米)甲車所用時間1680÷60+1680÷80=49 (小時),乙車用去的時間為1680×2÷70=48 (小時),甲乙所用的時間比為49:48.
3.A、B兩地間有一座橋,甲、乙兩人分別從A、B兩地同時出發,3小時后在橋上相遇。如果甲加快速度,每小時多行2千米,而乙提前0.5小時出發,則仍舊在橋上相遇。如果甲延遲0.5小時出發,乙每小時少走2千米,還會在橋上相遇,則A、B兩地相距多少千米?
解答: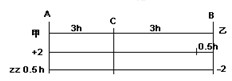
第二次,甲到橋時間為3-0.5=2.5h。 V甲×3=(V甲+2)×2.5 所以V甲=10km/h。
第三次,乙到橋時間為3+0.5=3.5h。 V乙×3=(V乙-2)×3.5 所以V甲=14km/h。
所以(10+14)×3=72(千米)
4.甲、乙兩車分別從A、B兩地同時出發相向而行,5小時后相遇在C點。如果甲車速度不變,乙車每小時多行5千米,且兩車還從A、B兩地同時出發相向而 行,則相遇地點距C點10千米,如果乙車速度不變,甲車每小時多行5千米,且兩車還從A、B兩地同時出發相向而行,則相遇地點距C點5千米。甲車原來的速 度?
解答:第二次第三次速度和不變,所以相遇時間相同。
對甲,(10+5)÷5=3(h)
對比第一次第二次,甲的路程,
2小時走10km,所以甲速度為5km/h。



