奧數(shù)題及答案:
學(xué)而思奧數(shù)天天練欄目每日精選中等、高等難度試題各一道。中難度試題適合一些有過(guò)思維基礎(chǔ)訓(xùn)練、考題學(xué)習(xí)經(jīng)歷,并且?jiàn)W數(shù)成績(jī)中上的學(xué)生。高難度試題立足于杯賽真題、綜合應(yīng)用和加深各知識(shí)點(diǎn),適合一些志在競(jìng)賽中奪取佳績(jī)的學(xué)生。
·本周試題由學(xué)而思奧數(shù)名師精選、解析,以保證試題質(zhì)量。
·每周末,我們將一周試題匯總為word版本試卷,您可下載打印或在線閱讀。
·每道題的答題時(shí)間不應(yīng)超過(guò)15分鐘。答案明日公布!
【枚舉法】
1、難度:★★★★
有一些三位數(shù)的各位數(shù)字都不是0,且各位數(shù)字之和為6,這樣的三位數(shù)共有多少個(gè)?
【詳解】對(duì)于不同情況進(jìn)行枚舉分析
個(gè)位為1,那么十位+百位=5,所以有(1,4)、(2,3)、(3,2)、(4,1)四種情況;
個(gè)位為2,那么十位+百位=4,所以有(1,3)、(2,2)、(3,1)三種情況;
個(gè)位為3,那么十位+百位=3,所以有(1,2)、(2,1)二種情況;
個(gè)位為4,那么十位+百位=2,所以有(1,1)一種情況;
個(gè)位為5或6,那么十位+百位=1或0 ,不可能;
綜上所述:這樣的三位數(shù)共有1+2+3+4=10種情況
2、難度:★★★★★
甲、乙、丙三個(gè)人傳球,第一次傳球是由甲開(kāi)始,將球傳給乙或丙……經(jīng)過(guò)4次傳球后,球正好回到甲手中,那么一共有多少種不同的傳球方式?
【詳解】學(xué)會(huì)用樹(shù)形圖的方法
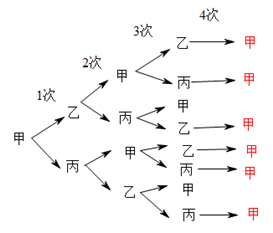
由圖可知:一共有6種不同的傳球方式。



