學而思奧數天天練欄目每日精選中等、高等難度試題各一道。中難度試題適合一些有過思維基礎訓練、考題學習經歷,并且奧數成績中上的學生。高難度試題立足于杯賽真題、綜合應用和加深各知識點,適合一些志在競賽中奪取佳績的學生。
·本周試題由學而思教研部《小學奧數系統總復習》編者趙永明老師精選、解析,以保證試題質量。
·每周末,我們將一周試題匯總為word版本試卷,您可下載打印或在線閱讀。
·每道題的答題時間不應超過15分鐘。答案明日公布!
【數論專題】
1.難度:★★★
“民間流傳著一則故事--‘韓信點兵’.秦朝末年,楚漢相爭.一次,韓信將1500名將士與楚王大將李鋒交戰.苦戰一場,楚軍不敵,敗退回營,漢軍也死傷四五百人.忽有后軍來報,說有楚軍 騎兵追來,韓信便急速點兵迎敵.他命令士兵3人一排,結果多出2名;接著命令士兵5人一排,結果多出3名;他又命令士兵7人一排,結果又多出2名.韓信馬 上向將士們宣布:我軍有1073名勇士,敵人不足五百,我們居高臨下,以眾擊寡,一定能打敗敵人.”根據故事中的條件,你知道韓信怎么算出有名將士的嗎?
【分析】也就是說:一個自然數在1000和1100之間,除以3余2,除以5余3,除以7余2,求符合條件的數.
方法一:由于除以3余2,除以7余2,所以滿足一、三兩個條件的最小自然數為3*7+2=23 ,而23也恰好滿足除以5余3,所以23再加[3,5,7]=105的倍數即符合要求,23+105*10=1073.
方法二:我們先找出被3除余2的數:2,5,8,11,14,17,20,23,26,29,32,35,38、41,44……;
被5除余3的數:3,8,13,18,23,28,33,38,43,48,53,58……;
被7除余2的數:2,9,16,23,32,37,44,51…….
三個條件都符合的最小的數是23,以后的是一次加上3,5,7的公倍數,直到加到1000和1100之間.結果是23+105*10=1073.具體到實際的做題過程中時,從較大的除數開始做會方便一些.
方法三:利用中國剩余定理求解[5,7]*2*2+[3,7]*3+[3,5]*2=233,將題目轉化為:求233加上105的倍數在1000~1100之間的數.通過嘗試可以求出這個數是233+105*8=1073.
2.難度:★★★
用a,b,c,d,e分別代表五進制中5個互不相同的數字,如果 ,
,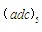 ,
,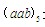 是由小到大排列好的連續正整數,那么
是由小到大排列好的連續正整數,那么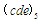 所表示的正整數寫成十進制表示的是多少?
所表示的正整數寫成十進制表示的是多少?
【分析】先將非十進制數化為十進制數,然后依題意列方程,求出方程的解.這樣,就不難求出問題的答案了.
因為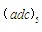 -
-  =1,所以c-e=1 .又因為
=1,所以c-e=1 .又因為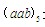 -
- 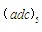 =1,即(5a+b)-(5d+c)=1,所以5(a-d)+(b-c)=1
=1,即(5a+b)-(5d+c)=1,所以5(a-d)+(b-c)=1
由于a,b,c,d,e都是0至4之間的不同整數,從而可以推知:a-d=1 ,c-b=4 .
經檢驗,得 c=4,b=0 ,e=3 ,a=2 ,d=1 ,于是有
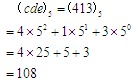
-------------------------------------------------------------------------------------
《小學奧數系統總復習》 圖書簡介
 |
《小學奧數系統總復習》分 上下兩冊,涵蓋了奧數中8大專題,共設21講。每講設置4大模塊,即闖關目標、賽前熱身、實戰演練和逐級闖關,構建了完整的奧數知識體系,全面覆蓋小學奧 數知識。此外,本書對部分經典例題錄制了視頻,免費贈送給各位學員。本書附有2010年和2011年的北京集訓隊選拔試題,為本書增加了新的亮點。 為了讓大家更好的獲得知識、理解知識,本書設有論壇交流環節,讀者可以登錄E度論壇點擊進入圖書答疑帖,即可實現在線提問、交流心得,名師天天坐鎮論壇,等你來交流! |



