ĪĪĪĪīW(xu©”)Č°╦╝ŖWöĄ(sh©┤)╠ņ╠ņŠÜÖ┌─┐├┐╚šŠ½▀xųąĄ╚ĪóĖ▀Ą╚ļyČ╚įćŅ}Ė„ę╗Ą└ĪŻųąļyČ╚įćŅ}▀m║Žę╗ą®ėą▀^╦╝ŠS╗∙ĄA(ch©│)ė¢(x©┤n)ŠÜĪó┐╝Ņ}īW(xu©”)┴Ģ(x©¬)Įø(j©®ng)ÜvŻ¼▓óŪęŖWöĄ(sh©┤)│╔┐āųą╔ŽĄ─īW(xu©”)╔·ĪŻĖ▀ļyČ╚įćŅ}┴óūŃė┌▒Ł┘ÉšµŅ}ĪóŠC║Žæ¬(y©®ng)ė├║═╝ė╔ŅĖ„ų¬ūR(sh©¬)³c(di©Żn)Ż¼▀m║Žę╗ą®ųŠį┌Ėé┘ÉųąŖZ╚Ī╝č┐āĄ─īW(xu©”)╔·ĪŻ
ĪĪĪĪ·▒Šų▄įćŅ}ė╔īW(xu©”)Č°╦╝Į╠čą▓┐ĪČąĪīW(xu©”)ŖWöĄ(sh©┤)ŽĄĮy(t©»ng)┐éÅ═(f©┤)┴Ģ(x©¬)ĪĘŠÄš▀░ūüåŠĻ└ŽÄ¤Š½▀xĪóĮŌ╬÷Ż¼ęį▒ŻūCįćŅ}┘|(zh©¼)┴┐ĪŻ
ĪĪĪĪ·├┐ų▄─®Ż¼╬ęéāīóę╗ų▄įćŅ}ģR┐é×ķword░µ▒ŠįćŠĒŻ¼─·┐╔Ž┬▌d┤“ėĪ╗“į┌ŠĆķåūxĪŻ
ĪĪĪĪ·├┐Ą└Ņ}Ą─┤Ņ}Ģr(sh©¬)ķg▓╗æ¬(y©®ng)│¼▀^15ĘųńŖĪŻ┤░Ė├„╚š╣½▓╝ŻĪ
ĪŠėŗ(j©¼)öĄ(sh©┤)īŻŅ}Ī┐
ĪĪĪĪ1Ż«ļyČ╚Ż║Ī’Ī’Ī’
ĪĪĪĪį┌Ž┬łDųąŻ¼ė├╦«ŲĮ╗“š▀┤╣ų▒Ą─ŠĆČ╬▀BĮėŽÓÓÅĄ─ūų─ĖŻ¼«ö(d©Īng)čžų°▀@ą®ŠĆČ╬ąąū▀Ģr(sh©¬)Ż¼š²║├Ų┤│÷"APPLE"Ą─┬ĘŠĆ╣▓ėąČÓ╔┘ŚlŻ┐
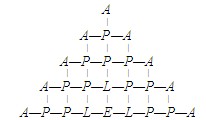
ĪĪĪĪĪŠĮŌ╬÷Ī┐ꬎļŲ┤│÷ėóšZ"APPLE"Ą─å╬į~Ż¼▒žĒÜ░┤šš"A→P→P→L→E"Ą─┤╬ą“Ų┤īæŻ«į┌łDųąĄ─├┐ę╗ĘNŲ┤īæĘĮ╩ĮČ╝ī”æ¬(y©®ng)ų°ę╗ŚlūŅČ╠┬ĘÅĮŻ«╚ńŽ┬łD╦∙╩ŠŻ¼▀\(y©┤n)ė├ś╦(bi©Īo)╠¢(h©żo)Ę©įŁ└Ēś╦(bi©Īo)╠¢(h©żo)Ą├│÷╣▓ėą31ĘN▓╗═¼Ą─┬ĘÅĮŻ«
ĪĪĪĪ2Ż«ļyČ╚Ż║Ī’Ī’Ī’Ī’
ĪĪĪĪī”ę╗éĆ(g©©)ūį╚╗öĄ(sh©┤)ū„╚ńŽ┬▓┘ū„Ż║╚ń╣¹╩Ū┼╝öĄ(sh©┤)ät│²ęį2Ż¼╚ń╣¹╩ŪŲµöĄ(sh©┤)ät╝ė1Ż¼╚ń┤╦▀M(j©¼n)ąąų▒ĄĮĄ├öĄ(sh©┤)×ķ1▓┘ū„═Żų╣Ż«å¢Įø(j©®ng)▀^9┤╬▓┘ū„ūā?y©Łu)?Ą─öĄ(sh©┤)ėąČÓ╔┘éĆ(g©©)Ż┐
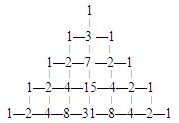
ĪĪĪĪĪŠĮŌ╬÷Ī┐┐╔ęįŽ╚ćLįćę╗Ž┬Ż¼Ą╣═ŲĄ├│÷Ž┬├µĄ─łDŻ║
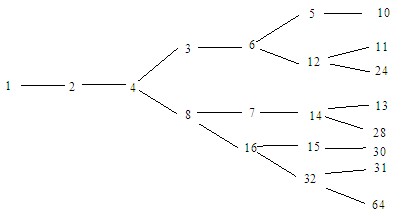
ĪĪĪĪŲõųąĮø(j©®ng)1┤╬▓┘ū„ūā?y©Łu)?Ą─1éĆ(g©©)Ż¼╝┤2Ż¼
ĪĪĪĪĮø(j©®ng)2┤╬▓┘ū„ūā?y©Łu)?Ą─1éĆ(g©©)Ż¼╝┤4Ż¼
ĪĪĪĪĮø(j©®ng)3┤╬▓┘ū„ūā?y©Łu)?Ą─2éĆ(g©©)Ż¼╩Ūę╗Ųµę╗┼╝Ż¼
ĪĪĪĪęį║¾░l(f©Ī)¼F(xi©żn)Ż¼├┐éĆ(g©©)┼╝öĄ(sh©┤)┐╔ęįūā│╔ā╔éĆ(g©©)öĄ(sh©┤)Ż¼Ęųäe╩Ūę╗Ųµę╗┼╝Ż¼├┐éĆ(g©©)ŲµöĄ(sh©┤)ūā?y©Łu)ķę╗éĆ(g©©)┼╝öĄ(sh©┤)Ż¼ė┌╩ŪŻ¼Įø(j©®ng)1Īó2Īó…┤╬▓┘ū„ūā?y©Łu)?Ą─öĄ(sh©┤)Ą─éĆ(g©©)öĄ(sh©┤)ę└┤╬×ķŻ║1Ż¼1Ż¼2Ż¼3Ż¼5Ż¼8Ż¼…
ĪĪĪĪ▀@ę╗┤«?d©Īng)?sh©┤)ųąėąéĆ(g©©)╠ž³c(di©Żn)Ż║ūįĄ┌╚²éĆ(g©©)ķ_╩╝Ż¼├┐ę╗éĆ(g©©)Ą╚ė┌Ū░ā╔éĆ(g©©)Ą─║═Ż¼╝┤╝┤Įø(j©®ng)▀^9┤╬▓┘ū„ūā?y©Łu)?Ą─öĄ(sh©┤)ėą34éĆ(g©©).
ĪĪĪĪ×ķ╩▓├┤╔Ž├µĄ─ęÄ(gu©®)┬╔╩Ūš²┤_Ą──žŻ┐
ĪĪĪĪĄ└└Ēę▓║▄║åå╬.įO(sh©©)Įø(j©®ng)▀^n┤╬▓┘ū„ūā?y©Łu)?Ą─öĄ(sh©┤)Ą─éĆ(g©©)öĄ(sh©┤)×ķ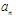 ,ät
,ät =1Ż¼
=1Ż¼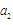 =1Ż¼
=1Ż¼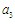 =2Ż¼…
=2Ż¼…
ĪĪĪĪÅ─╔Ž├µĄ─łD┐┤│÷Ż¼ ▒╚
▒╚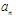 ┤¾.
┤¾.
ĪĪĪĪę╗ĘĮ├µŻ¼├┐éĆ(g©©)Įø(j©®ng)▀^n┤╬▓┘ū„ūā?y©Łu)?Ą─öĄ(sh©┤)Ż¼│╦ęį2Ż¼Š═Ą├│÷ę╗éĆ(g©©)┼╝öĄ(sh©┤)Ż¼Įø(j©®ng)▀^n+1┤╬▓┘ū„ūā?y©Łu)?Ż╗Ę┤▀^üĒŻ¼├┐éĆ(g©©)Įø(j©®ng)▀^n+1┤╬▓┘ū„ūā?y©Łu)?Ą─┼╝öĄ(sh©┤)Ż¼│²ęį2Ż¼Š═Ą├│÷ę╗éĆ(g©©)Įø(j©®ng)▀^n┤╬▓┘ū„ūā?y©Łu)?Ą─öĄ(sh©┤).╦∙ęįĮø(j©®ng)▀^n┤╬▓┘ū„ūā?y©Łu)?Ą─öĄ(sh©┤)┼cĮø(j©®ng)▀^n+1┤╬▓┘ū„ūā?y©Łu)?Ą─┼╝öĄ(sh©┤)ŪĪ║├ę╗śėČÓ.Ū░š▀Ą─éĆ(g©©)öĄ(sh©┤)╩Ū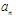 ,ę“┤╦║¾š▀ę▓╩Ū
,ę“┤╦║¾š▀ę▓╩Ū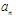 éĆ(g©©).
éĆ(g©©).
ĪĪĪĪ┴Ēę╗ĘĮ├µŻ¼├┐éĆ(g©©)Įø(j©®ng)▀^n┤╬▓┘ū„ūā?y©Łu)?Ą─┼╝öĄ(sh©┤)Ż¼£p╚ź1Ż¼Š═Ą├│÷ę╗éĆ(g©©)ŲµöĄ(sh©┤)Ż¼╦³Įø(j©®ng)▀^n+1┤╬▓┘ū„ūā?y©Łu)?Ż¼Ę┤▀^üĒ.├┐éĆ(g©©)Įø(j©®ng)▀^n+1┤╬▓┘ū„ūā?y©Łu)?Ą─ŲµöĄ(sh©┤)Ż¼╝ė╔Ž1Ż¼Š═Ą├│÷ę╗éĆ(g©©)┼╝öĄ(sh©┤)Ż¼╦³Įø(j©®ng)▀^n┤╬▓┘ū„ūā?y©Łu)?.╦∙ęįĮø(j©®ng)▀^n┤╬▓┘ū„ūā?y©Łu)?Ą─┼╝öĄ(sh©┤)Įø(j©®ng)▀^n+1┤╬▓┘ū„ūā?y©Łu)?Ą─ŲµöĄ(sh©┤)ŪĪ║├ę╗śėČÓ.
ĪĪĪĪČ°ė╔╔Ž├µ╦∙šfŻ¼Ū░š▀Ą─éĆ(g©©)öĄ(sh©┤)Š═╩Ū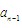 ,ę“┤╦║¾š▀ę▓╩Ū
,ę“┤╦║¾š▀ę▓╩Ū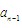 .
.
ĪĪĪĪĮø(j©®ng)▀^n+1┤╬▓┘ū„ūā?y©Łu)?Ą─öĄ(sh©┤)Ż¼Ęų×ķ┼╝öĄ(sh©┤)ĪóŲµöĄ(sh©┤)ā╔ŅÉŻ¼╦∙ęį =
=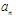 +
+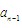 Ż¼╝┤╔Ž├µ╦∙šfĄ─ęÄ(gu©®)┬╔Ą─┤_│╔┴ó.
Ż¼╝┤╔Ž├µ╦∙šfĄ─ęÄ(gu©®)┬╔Ą─┤_│╔┴ó.
 ŠÄ▌ŗ═Ų╦]Ż║
ŠÄ▌ŗ═Ų╦]Ż║
-------------------------------------------------------------------------------------
ĪČąĪīW(xu©”)ŖWöĄ(sh©┤)ŽĄĮy(t©»ng)┐éÅ═(f©┤)┴Ģ(x©¬)ĪĘ łDĢ°║åĮķ
 |
ĪČąĪīW(xu©”)ŖWöĄ(sh©┤)ŽĄĮy(t©»ng)┐éÅ═(f©┤)┴Ģ(x©¬)ĪĘĘų ╔ŽŽ┬ā╔āįŻ¼║Ł╔w┴╦ŖWöĄ(sh©┤)ųą8┤¾īŻŅ}Ż¼╣▓įO(sh©©)21ųvĪŻ├┐ųvįO(sh©©)ų├4┤¾─ŻēKŻ¼╝┤ĻJĻP(gu©Īn)─┐ś╦(bi©Īo)Īó┘ÉŪ░¤ß╔ĒĪóīŹ(sh©¬)æ(zh©żn)č▌ŠÜ║═ų╝ē(j©¬)ĻJĻP(gu©Īn)Ż¼śŗ(g©░u)Į©┴╦═Ļš¹Ą─ŖWöĄ(sh©┤)ų¬ūR(sh©¬)¾wŽĄŻ¼╚½├µĖ▓╔wąĪīW(xu©”)ŖW öĄ(sh©┤)ų¬ūR(sh©¬)ĪŻ┤╦═ŌŻ¼▒ŠĢ°ī”▓┐ĘųĮø(j©®ng)Ąõ└²Ņ}õøųŲ┴╦ęĢŅlŻ¼├Ō┘M(f©©i)┘ø(z©©ng)╦═ĮoĖ„╬╗īW(xu©”)åTĪŻ▒ŠĢ°ĖĮėą2010─Ļ║═2011─ĻĄ─▒▒Š®╝»ė¢(x©┤n)ĻĀ(du©¼)▀x░╬įćŅ}Ż¼×ķ▒ŠĢ°į÷╝ė┴╦ą┬Ą─┴┴³c(di©Żn)ĪŻ ×ķ┴╦ūī┤¾╝ęĖ³║├Ą─½@Ą├ų¬ūR(sh©¬)Īó└ĒĮŌų¬ūR(sh©¬)Ż¼▒ŠĢ°įO(sh©©)ėąšōē»Į╗┴„Łh(hu©ón)╣Ø(ji©”)Ż¼ūxš▀┐╔ęįĄŪõøEČ╚šōē»³c(di©Żn)ō¶▀M(j©¼n)╚ļłDĢ°┤ę╔╠¹Ż¼╝┤┐╔īŹ(sh©¬)¼F(xi©żn)į┌ŠĆ╠ßå¢ĪóĮ╗┴„ą─Ą├Ż¼├¹Ä¤╠ņ╠ņū°µé(zh©©n)šōē»Ż¼Ą╚─ŃüĒĮ╗┴„ŻĪ |



