決戰2013年小升初數學競賽解題密匙:整除問題(2)
來源:奧數網整理 2012-10-15 17:24:51

例 3 三個質數的和為 122,求這三個質數的乘積的最大值。 解:因為三個質數的和為 122 是偶數,所以這三個質數當中必定有一個數是偶數,另外兩個質數都是奇數。在質數中,2 是唯一的偶數,故三個質 數中有一個質數是 2。
另外兩個質數的和為定值(120),為使這兩個質數的乘積盡可能地大, 就要使該兩個質數的差值盡可能地小,因為 1202÷2=60,所以得到 59 和 61 兩個質數,是和為 120 且差為最小的兩個質數,它們的積也就最大。
綜合以上情況,和為 122 的三個質數中,以 2、59、61 這三個質數的乘 積最大,最大乘積為 2×59×61=7198。
答:三個質數的乘積的最大值是 7198。 說明:注意“如果兩個整數的和一定,那么當這兩個數的差值盡可能小時,其乘積最大”。
例如,和為 11 的兩個整數有如下五種情況:1+10、2+9、3+8、4+7、5+6,相對應的乘積是 10、18、24、28、30,通過比較,可得“和為 11,其 積最大的兩個整數是 5 和 6”。
例 4 如果 325×472+765×895×( )的積的最后五個數字都是零, 那么括號內填入的自然數最小可以是多少?(上海市 1989 年小學六年級數學比賽題)
解:
要使五個數的連乘積的最后五個數字都是 0,這個連乘積一定是 100000 的倍數,把 100000 分解質因數:100000=25×55。
說明要使連乘積的末尾有五個零,因數中至少應該有五個2 和五個5。因為325=52×13, 765=3×5×51,472=23×59,895=5×179四個數的乘積里一共包含了 4 個 5 和 3 個 2,必須要再乘以兩個 2 和一 個 5,所以括號里應填 22×5=20。
答:在括號內最小可以是 20。
例 5 360 這個數的約數有多少個?這些約數的和是多少?(第三屆華羅庚金杯賽決賽題)
解:把 360 分解質因數是:360=23×32×5,所以 360 的任何一個約數都 是從三個質數 2、二個質數 3、一個質數 5 中取若干個出來相乘得到的。
23 的約數是 1、2、4、8(或 1、21、22、23);
32 的約數是 1、3、9(或 1、31、32);
5 的約數是 1、5(或 1、51)。 如果我們把下面的式子
(l+2+4+8)×(1+3+9)×(1+5) 展開成一個和式,和式中的每一個加數都是在每個括號里各取一個數相乘的 積。由前面的分析可得,360 的任一個約數都恰好是這個展開式中的一個加 數。由于第一個括號里有 4 個數,第二個括號里有 3 個數,第三個括號里有2 個數,所以這個展開式中的加數個數是 4×3×2=24,這就是 360 的約數的總個數,這些約數是:
1×1×1=1,2×1×1=2,4×1×1=4,8×1×1=8,
1×1×5=5,2×1×5=10,4×1×5=20,8×1×5=40,
1×3×1=3,2×3×1=6,4×3×1=12,8×3×1=24,
1×3×5=15,2×3×5=30,4×3×5=60,8×3×5=120,
1×9×1=9, 2×9×1=18,4×9×1=36,8×9×1=72,
1×9×5=45,2×9×5=90,4×9×5=180,8×9×5=360。
(你能知道上面每個等式中,三個數相乘的由來嗎?)
另一方面,360 的所有約數的和就等于這個展開式的和,也就是(1+21+22+23)×(1+31+32)×(1+51)=1170。
答: 360 的約數有 24 個,這些約數的和是 1170。
說明:本題中的二個問題的解法具有一般性,并由此可以得出下面二個結論。
若 自然數 N 可以分解質因數為:
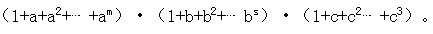
(其中 a、b、C 為不同的質數,m、s、t 為自然數), 則(1)自然數 N 的約數的總個數是(m+1)·(s+1)·(t+1);
(2)自然數 N 的所有約數的總和是

以上兩個結論可以推廣到一般的情況。
例 6 A、B 兩數都只含有質因數 3 和 5,它們的最大公約數是 75,已知 A 有 12 個約數,B 有 10 個約數,那么 A、B 兩數的最小公倍數是多少?
解:因為 A、B 兩數都只含有質因數 3 和 5,所以設 A=3m·5n,B=3s·5t。 因為 A、B 兩數的最大公約數是 75=3×52,所以,n≥2,t≥2。
又因為 A 有 12 個約數,根據例 8 后的說明可得(m+1)
·(n-1)=12=(1 十 1)·(5+1)=(2+1)·(3+1)=(3+1)
·(2+1)。所以 A 有三種可能:
3×55 或 32×53 或 33×52。 同理,因為乙有 10 個約數,可得
(s+1)·(t+1)=10=(1 十 1)·(4+1), 所以 B=3×54=1875。
由于 A、B 的最大公約數是 3×52,所以 A 只能是 33×52=673。這樣可得 A、B 兩數的最小公倍數是 33×54=16875。
答:A、B 兩數的最小公倍數是 16875。
相關文章
- 小學1-6年級作文素材大全
- 全國小學升初中語數英三科試題匯總
- 小學1-6年級數學天天練
- 小學1-6年級奧數類型例題講解整理匯總
- 小學1-6年級奧數練習題整理匯總
- 小學1-6年級奧數知識點匯總
- 小學1-6年級語數英教案匯總
- 小學語數英試題資料大全
- 小學1-6年級語數英期末試題整理匯總
- 小學1-6年級語數英期中試題整理匯總
- 小學1-6年語數英單元試題整理匯總





